Examen de Sémantique des programmes concurrents

Examen de Sémantique des programmes concurrents du 19 janvier 2001

Tous documents autorisés. Durée 2h.

Première partie

Exercice 1 (Automates et langages réguliers)

Question 1 L'un des deux sous ensembles de {a,b,$}* est régulier et l'autre ne l'est pas. Lequel est régulier ? Le démontrer (en exhibant un automate et en utilisant le lemme de la pompe). #a(x) désigne le nombre de a dans la chaîne x.
{xy / x,y Î {a,b}*, #a(x) = #bx)}
{x$y} / x,y Î {a,b}*, #a(x) = #bx)}

Question 2 Montrer que l'ensemble
PRIMES = {a^p / p est premier}
n'est pas régulier.

Dans les deux exercices qui suivent, vous pouvez faire une modélisation par des systèmes de transition avec produit synchronisé ou bien CCS.

Exercice 2 (Modélisation)

On souhaite modéliser un ensemble de n processus "lecteurs" et un ensemble de k processus "écrivains" cherchant à accéder un fichier commun. Il doivent respecter les règles suivantes :

un seul écrivain peut accéder au fichier à la fois,
il ne peut y avoir d'écrivain et de lecteur en même temps mais plusieurs lectures concurrentes sont possibles.

Question 3 Modéliser un tel système en considérant les deux variantes suivantes :

proposer une solution sans traitement équitable : les rédacteurs ou les écrivains peuvent monopoliser le fichier,
proposer une solution plus équitable où un lecteur ne peut lire que s'il n'y a pas de demande d'écriture.

Question 4 Construire le graphe d'état dans le cas de la première modélisation lorsque n=2 et k=2.

Exercice 3 (Modélisation)
On cherche à modéliser le "diner des philosophes" : quatres philosophes assis autour d'une table mangent des spaghettis. Devant chaque philosophes se trouve une assiette et une fourchette entre chaque assiette. Pour manger, le philosophe a besoin de deux fourchettes. Dès qu'il a fini de manger, il repose ses deux fourchettes.
Modéliser un tel système en considérant les deux variantes suivantes :

s'il ne peut prendre qu'une seule des deux fourchettes, que peut-il se passer ? Justifiez votre réponse. Vous pourrez, pour cela, construire le graphe d'état du système ou exprimer cette propriété par une expression régulière.
proposez une solution sans interblocage et donnez son graphe d'état.

Deuxième partie

On s'intéresse au problèe suivant : un ensemble de processus partagent une ressource (par exemple de la mémoire). Il y a initialement K exemplaires de cette ressource. Les processus, initialement au repos, peuvent décider de travailler (transition s) puis reviennent au repos (transition w). Au repos, un processus X peut décider d'acquérir un exemplaire supplémentaire de la ressource. Pour cela il franchit les transitions tg1, tg2, tg3. Il peut aussi décider de libérer un exemplaire de la ressource et il franchit alors les transitions tr1, tr2, tr3. Ce comportement est décrit par le modèle de la figure 1. Un certain nombre de problème se posent que l'on va essayer de résoudre. Pour cela on commence par appliquer une série de réductions sur le modèle initial. On obtient successivement les réseaux des figures 2 et 3.

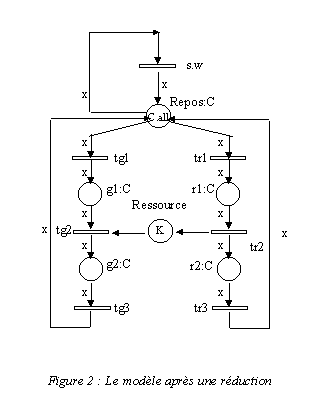
Question 5 Quelles réductions ont été appliquées ? (vous justifierez brièvement chacune de ces réductions)

Question 6 Pour quelles propriétés les modèles de lafigure 1 et de la figure 3 sont-ils équivalents et peut-on appliquer d'autres réductions sur le modèle de la figure 3 ?

Après un examen rapide du modèle réduit, vous constatez un problème su une évolution potentiellement aberrate du marquage de la place Ressource.

Question 7 Quel est ce problème ?

Afin de le corriger, vous rajoutez au modèle une nouvelle place Compte initialement non marquée (voi le réseau de la figure 4)

Question 8 Quelle interprétation simple pouvez-vous donner à cette nouvelle place ?
On utilise un outil pour calculer les invariants du modèle et on obtient les sommes formelles suivantes :

Ressources + S_xÎCCompte(x) = K
"xÎC, Repos(x) + g1(x) = 1
S_xÎCRepos(x) + S_xÎCg1(x) = N

Question 9Démontrez en utilisant ces invariants que le problème évoqué plus haut n'est plus présent dans le modèle de la figure 4.

On va maintenant résoudre l'autre problème important de cette modélisation. Pour cela on calcule les verrous du réseau (de la figure 4) et on obtient comme verrou strict l'ensemble S = {Ressource U_xÎC Repos(x)}

Question 10 Montrez que ce verrou peut se vider. Qu'en déduisez vous sur la vivacité du réseau ?

On ajoute alors une nouvelle place au réseau (place Contrôle) dont le marquage initial est S_xÎCk_x. <x> (ce qui signifie qu'il y a pour tout x, k_x fois la couleur x dans cette place, les k_x pouvant être différents. Le rôle de cette nouvelle place est de garantir qu'un processus x ne pourra détenir qu'au plus k_x exemplaires de la ressource à un moment donné.

Question 11 Intégrer cette place dans le réseau précédent (vous modifierez le réseau fourni en annexe).

Si vous avez corrigé le probème à l'aide de cette nouvelle place, la somme formelle suivante correspond à un invariant de votre modèle :
"xÎC, Contrôle(x) + g1(x) + Compte(x) = k_x

Question 12 A l'aide de cet invariant et des invariants calculés précédemment, donnez une condition nécessaire et suffisante liant K, N et les k_x garantissant que le verrou S ne peut se vider. Sous quelles hypothèses le problème soulevé à la question 7 est-il alors résolu ?

Question 13 Donnez en Ada ou en Java une implémentation de la partie serveur du dernier réseau (avec les corrections des problèmes évoqués). Ce serveur devra en particulier offrir deux entrées Get et Release (ou deux méthodes Java) permettant aux clients de prendre ou de relâcher un exemplaire de la ressource. Il gérera également les exemplaires disponibles de la ressource.

Annexe

Réseau à compléter et à rendre avec votre copie.